Velocity of Money

I wanted to follow up on Menzie’s recent observations about what’s been happening to the supply and demand for money.

These discussions are sometimes conducted in terms of the following equation:

MV = PY.

Here M is a measure of the money supply, V its velocity, and nominal GDP is written as the product of the overall price level (P) with real GDP (Y). We have direct measurements on nominal GDP. And once we agree on a definition of the money supply (no trivial matter), we have a number for M. But where do we come up with data on this concept of the velocity of money, V?

The answer is, we don’t have independent measures of the velocity of money. So if people talk about velocity as something they could measure, they’re just referring to the value of V that makes the above equation true. That is, we measure the velocity of money from

V = PY/M.

As alluded to above, different people come up with different answers for how we should measure the money supply. One measure is M1, whose key components include currency held by the public and checkable deposits. Another measure is the monetary base, which is currency held by both banks and the public plus deposits banks hold in their accounts with the Federal Reserve. So we could use M1 as the value for M in the above equation, and call the resulting value for V the “velocity of M1”. Or we could put the monetary base in for M, and call the resulting V the “velocity of the monetary base”. You get the idea– use your favorite M to get your favorite V.

Arnold Kling, for example, proposed that we might use for M the quantity of marbles.

Which perhaps sounds a little silly. Even if there’s no particular relation between the quantity of marbles and the stuff we care about (inflation and real GDP), you could still go ahead and use the equation above to define the velocity of marbles. But what you’d find is that when marbles go up, the marble velocity goes down, and it makes no difference for output or inflation.

OK, so let’s look at the velocity of M1. It turns out to look a lot like you’d expect the velocity of marbles to behave– when M1 goes up, the velocity of M1 goes down by an almost exactly offsetting amount. Here’s an update of a graph that I presented a year ago:

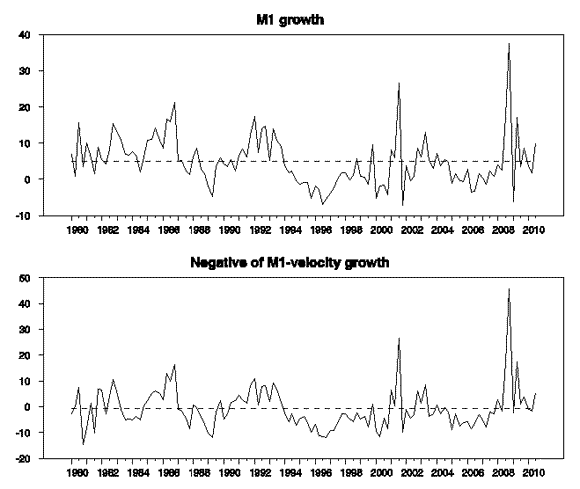
Top panel: annual growth rate of M1, 1980:Q1 to 2010:Q3. Bottom panel: annual growth rate of the ratio of M1 to nominal GDP. Horizontal line in each figure is drawn at the historical average for that series.

So maybe we’d be better off using the monetary base as our value for “M”? I don’t think so.

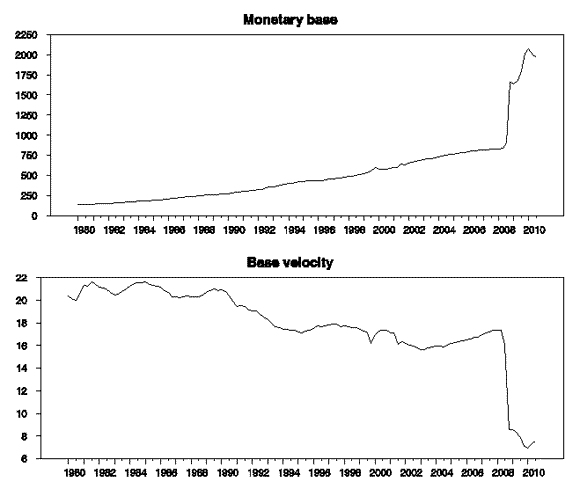
Top panel: level of monetary base, 1980:Q1 to 2010:Q3. Bottom panel: velocity of base

Obviously the interest in an equation like MV = PY comes not from using it as a definition of V for some arbitrary choice of M. Instead there must be some kind of behavioral idea, such as that there is some desired value of M1, or monetary base, or marbles, that people want to hold. Suppose it was the case that to a first approximation, this desired quantity was essentially proportional to nominal GDP. If that were true, we would see the graphs of V above behaving roughly as constants instead of simply tracking the inverse of whatever happens to M.

Now, I think it is true that, in normal times, nominal GDP is one of the most important determinants of the demand for M1 or the monetary base. In the absence of other factors changing these demands, there certainly is a connection between money growth and inflation, and you do find a correlation if you look at much longer horizons than the quarterly changes plotted above.

But conditions at the moment are far from normal. In particular, something quite remarkable has happened to the demand for the monetary base. In the current environment, banks have shown themselves to be indifferent between holding reserves (a risk-free way to earn a modest interest rate from the Fed) and making other uses of overnight funds. For this reason, the demand for reserves, and with it the demand for the monetary base, has ballooned without any corresponding changes in output or inflation.

Some people felt I was making a sophistic distinction in emphasizing that the Fed is creating reserves as opposed to printing money ([1], [2]). But I maintain this is a critical distinction. The demand for reserves has increased by a trillion dollars since 2008. The demand for currency held by the public has not. The supply of reserves could therefore increase a trillion dollars without causing inflation. The quantity of currency held by the public could not.

Now, the time will come when banks do see something better to do with these reserves, at which point the Fed will need to take appropriate measures in response, namely a combination of raising the interest rate paid on reserves and selling off some of the assets the Fed has been accumulating. This is of course a key long-term story that we will all be following with interest.

But someone who insists that inflation (P) must go up just because the monetary base (M) has risen may have lost their marbles.

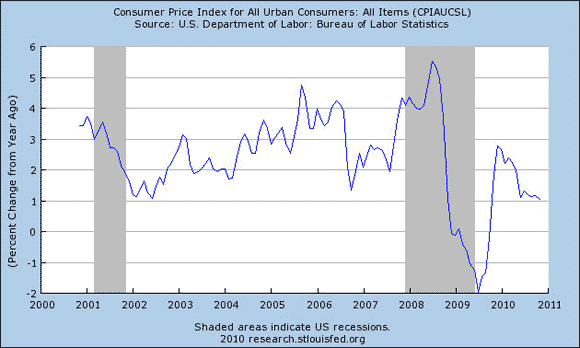
Source: FRED

Velocity of money

• Become A Funded Futures Trader