I have been writing recently ([1], [2]) about my paper Crunch Time: Fiscal Crises and the Role of Monetary Policy, co-authored with David Greenlaw (Managing Director and Chief U.S. Fixed Income Economist for Morgan Stanley), Peter Hooper (Managing Director and Chief Economist for Deutsche Bank Securities Inc.), and Frederic Mishkin (professor at Columbia University and former governor of the Federal Reserve). Our paper has generated some interesting discussion by Paul Krugman and Matthew O’Brien, among others, to which I’d like to respond.
Our paper presents 90 pages of analysis and evidence. In fact, in my previous Econbrowser entries, I still haven’t had a chance to touch on the role of monetary policy in dealing with these situations, which was one of our primary interests in the paper. I promise to bring these issues up in my next Econbrowser post. But it seems some readers were distracted by the criticisms raised by Krugman and O’Brien, or perhaps shared related concerns of their own. So I thought it might be best to take up those concerns now, and discuss the implications for monetary policy later.
Krugman and O’Brien focus entirely on a single subsection of our paper which reports results from statistical regressions that try to predict sovereign interest rates as functions of conditions that prevailed in a country during the preceding year. These regressions use a panel of 20 different countries followed for a period of 12 years. Krugman and O’Brien note correctly that 13 of these 20 countries are in the European currency union, and suggest, appealing to De Grauwe’s (2011) analysis of particular challenges facing the eurozone, that the experience of those 13 countries has no relevance for countries not in the eurozone.
Let me begin by discussing the econometric issues and then turn to the economic issues. Here are the results from one of the regressions in dispute:
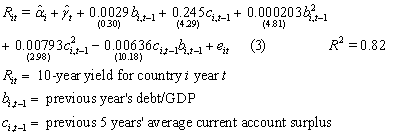
Note first that the possibility that every country is different is already incorporated in our baseline regression model in the form of country fixed effects. The special characteristics that may make one country different from all the others are captured by the coefficients αi in the above equation. These represent 20 different numbers, with a different value for αi estimated for each country i in the sample. A special case of that specification is one in which the eurozone countries as a group are different from the non-eurozone countries as a group, that is, a regression in which there are two different parameters αeuro and αnoneuro. We instead estimate a much more general specification than that, allowing for 20 different values for αi instead of only two.
Thus our baseline assumption is that the effects in question will show up differently in different countries. We comment in detail in our paper, for example, on the fact that countries like the U.S. and Japan seem to have a significantly higher debt tolerance (in the form of big negative values for αi) than other countries. I should also mention that we allow for separate year fixed effects in the form of a different estimated value for γt for each year t in the sample. Our baseline assumption is that every country could be different and every year could be different.
By the way, one implication of this feature of our specification is that scatter diagrams such as those plotted by Krugman and O’Brien are not a valid device for seeing visually what is behind the estimated regression coefficients. To do this properly, the variables plotted on the axes should be deviations from within-country and within-year averages, not the raw data as is done in their figures. And while I am on the topic, I should point out that Krugman’s scatter diagram is unrepresentative of the relations underlying equation (3) above for a simpler reason: none of the data points plotted in Krugman’s figure were used at all in the estimation of equation (3). Instead, the points he plots are out-of-sample values, namely, 2012 interest rates. These came in after we had performed the estimation of (3). These data are consistent with equation (3), but were not used in any way in the estimation of (3).
It is true that we allowed for differences across countries only through differences in the intercept. One might argue more generally that countries differ not just in the intercept but in all of the slope coefficients as well, wishing to estimate a value for the coefficient on bi,t-1 and all the other variables that is a different coefficient for each country i. However much one might wish to do this, this would have been quite a pointless exercise, since one would then be trying to estimate 6 different parameters for each country from 12 total observations for that country. Even so, it would still be less general in one respect from our equation (3), in that the latter allows for changes in interest rates over time captured by the year fixed factors, whereas a single-country regression would not allow for time heterogeneity.
Or, perhaps Krugman and O’Brien would be willing to suppose that non-euro advanced economies as a group share the same slope coefficients, that is, share the same coefficients on variables like the debt and the current-account surplus, and then estimate those common coefficients from panel regressions like ours, with two different sets of slope coefficients, one for eurozone and another for other countries. O’Brien reports that when he tried to do this, he found no effects of debt. But if you chop the data set down to only a half-dozen countries, you’re going to need a longer time series if you hope to estimate the relation with any kind of precision.
There are plenty of other researchers who have done just that. For example, Ichiue and Shimuzu (2013) looked at a panel of 10 advanced economies over 1990-2010, of which Germany is the only eurozone member. They found that a one-percentage-point increase in debt-to-GDP, if matched by a 1-percentage-point increase in country external debt, was associated with a 3-basis-point increase in the 5-year-forward 10-year yield. Reinhart and Sack (2000) looked at the pre-euro G7 (1981-2000), and found that a 1-percentage-point increase in projected government-surplus-to-GDP was associated with a 12-basis-point decline in the 10-year over 3-month yield spread. If you want to insist that the only evidence relevant for the U.S. is historical U.S. data, let me point you to Laubach’s (2009) analysis of the effects on yields of changes in CBO budget projections over 1976-2006. He found that a 1-percentage-point increase in U.S. debt-to-GDP was associated with a 3-to-4-basis-point increase in the 5-year-forward 10-year rate. And if you’re willing also to look at evidence from emerging economies or go farther back in time, there are many, many other studies confirming the basic relation that Krugman and O’Brien want to insist couldn’t possibly apply to a country like the United States.
If you consider what equation (3) above implies for an advanced economy with moderate debt loads, it is quite consistent with most of the studies just mentioned. For example, if a country has debt-to-GDP of 60% and a balanced current account, equation (3) says that a 1-percentage-point increase in debt-to-GDP would be associated with a 2.7-basis-point increase in the 10-year yield.
Another indication that the recent problems in Europe are not just a reflection of problems with maintaining the euro is provided by the remarkable similarity between recent moves in interest rates and their behavior before establishment of the euro.
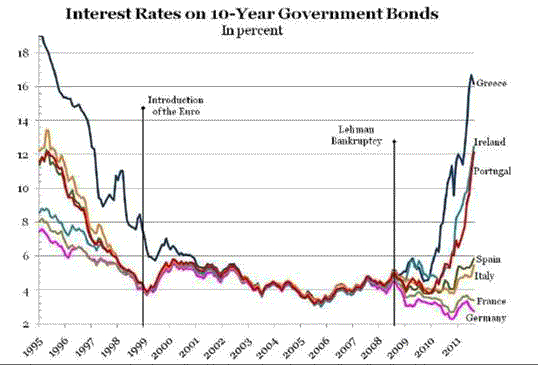
Source: BBC
It is true that you won’t find statistical confirmation of the nonlinearities reported in equation (3) if you confine yourself to recent experience in the major non-eurozone advanced economies. There’s a simple reason for that– these countries have not yet reached the tipping point in the dynamics of fiscal debt loads.
Are Krugman and O’Brien claiming that they never could? Do they maintain that U.S. debt could become an arbitrarily large multiple of GDP with no consequences for yields? If they acknowledge that there is a level of debt at which these effects would start to matter for the United States, what is their estimate of that level, and how did they arrive at it?
In our paper we offer our answer to these questions. We conclude that a country’s debt limit depends on its borrowing rate, its economic growth rate, and the fraction of GDP that the public is willing to commit to maintaining a permanent primary surplus– that is, government revenues minus spending on all items other than interest expense. If Krugman, O’Brien, or anybody else thinks they have some other answer, let them articulate it clearly and cleanly.
Whether a country is able to borrow in its own currency is completely irrelevant for the above calculation. Yes, it means the country likely won’t technically default on the debt, and could always create new money to pay off the creditors. But as Reis (2013) and Leeper (2013) have recently explained, printing money does not generate any magical resources with which to resolve a real fiscal shortfall. The central bank could create some more inflation, but anticipated inflation does nothing to alter the above determination of the limits on government debt. Anticipated inflation would just cause the nominal interest rate R and the nominal growth rate g to both increase by the same amount, and therefore would do nothing to change the net growth rate r = R – g which is the key parameter in our equation for sustainability (see for example equation (2) in Econbrowser March 6 or equation (8) in our paper).
It is true that an unanticipated inflation would succeed in bringing the real debt burden down. But as soon as creditors become concerned that this is the way the problem will be resolved, nominal rates will rise and the game between the government and lenders becomes precisely the one we model, vulnerable to exactly the tipping-point dynamics we highlight.
Krugman and O’Brien seem to assert with great confidence that these tipping-point dynamics could never matter for a country like the United States. I find no basis in either economic theory or historical experience to warrant such a conclusion. Their argument ultimately seems to boil down to, “it can’t happen, because it hasn’t happened yet.”
Or rather, because it hasn’t happened here yet.



Leave a Reply