The Job Shortfall: Then and Now

In an interesting post a couple weeks ago, Keith Hennessey critiques the President’s recent speech about employment growth, and presents the following graph, to highlight the gap between where employment is and where it “should” be.

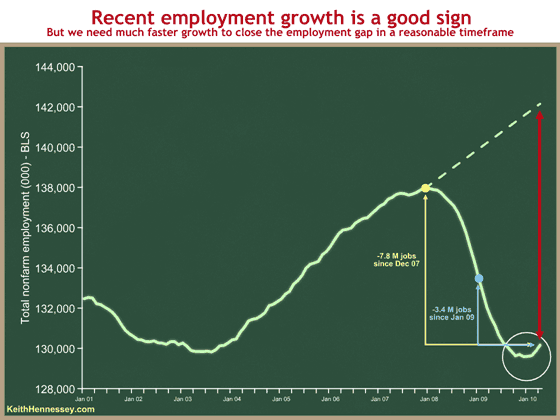
Figure 1: from Hennessey (May 20, 2010)

I’m not sure what the trend is in his graph; it appears to be estimated on the level of nonfarm payroll employment. I “eyeball” the length red line at about 11.7 jobs. The graph explicitly lists 3.4 million net job loss going from January 2009 to April 2010.

I thought it interesting to costruct a similar graph corresponding to the administration of Mr. Hennessey’s boss, President Bush (actually, he was my boss, too, for 5 months). The graph below incorporates the May employment release.

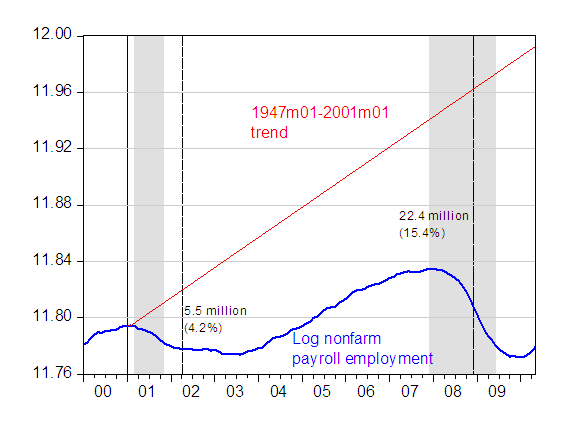
Figure 2: Log nonfarm payroll employment, in thousands (blue line), linear trend estimated over 1947M01-2001M01 period (red line). Gray shaded areas are NBER defined recession dates, assuming last recession ended 2009M06. Vertical line at beginning of Bush Administration (2001M01); vertical dashed line at April 2002 (corresponds in timing to Hennessey comparison); vertical dashed line at end of Bush Administration (2008M12). Source: BLS, May 2010 release, via FREDII, NBER, and author’s calculations.

At the corresponding point in his Administration, President Bush was down by 5.5 million from the 1947M01-2001M01 linear deterministic trend. Interestingly, by the end of his Administration, in December 2008, it was 22.4 million below trend. By the way, the estimated trend is 0.0018 per month; the shortfall would look worse if one used the 1991M04-2001M01 period to estimate the trend, since the estimated monthly rate of increase in log NFP is 0.0020).

The graph also highlights another interesting point: NFP only started rising on a sustained basis in September 2003, some 32 months after 2001M01.

A caveat: Log nonfarm payroll employment (NFP) does not appear to be trend stationary. In fact the ADF test with optimal lag length selected by AIC or BIC fails to reject the unit root null over the 1947M01-2010M05 period. Similarly for the Elliott-Rothenberg-Stock DF test. A Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test with trend stationarity null does reject at conventional levels. Estimating a very simple difference stationary process (i.e., an ARIMA(0,1,0) yields similar rate of increase, 0.0017 per month, versus the 0.0018 for a linear trend.

The point that log NFP is not characterized as trend stationary is well known. In fact, this is true for most macroeconomic time series — although for a long enough sample, one can find trend stationarity for US real GDP (see discussion of some very simple time series econometrics [1] [2] [3] [4]).

One can still do projections, either assuming difference stationarity (which, if Mr. Hennessey wanted to stay in the univariate context, would be more appropriate). Or one could appeal to a multivariate approach, such as cointegration. This would require taking a stand on what variables were cointegrated, and the stability of that relationship, but at least then one could talk about reversion — although then the reversion is to close the error correction term defined by the cointegrating relationship. For an example, see this post, which relies upon a GDP-employment cointegrating relationship.

That being said, I agree with Mr. Hennessey:

Instead, I’m trying to show that, while +290K jobs in April is a good number, and it is the most jobs created in any single month in four years, we need a much more rapid pace of net job creation for the foreseeable future to close the employment gap in a reasonable time frame. And the “best in four years” shouldn’t surprise you, as we should expect more jobs to be created during a recovery than when the economy is at or near full employment.

But I would add that we should probably move beyond simple univariate characterizations of trends in our policy discussions.

The Job Shortfall: Then and Now