An NBC News poll (in the field August 15-17) has just appeared, focusing on health care issues (findings for select items were released during the day, but a comprehensive article was not available until 6:30 Eastern). One finding that was reported during the day is as follows:
…43 percent say they favor a public option, versus 47 percent who oppose it. That’s a shift from last month’s NBC/Journal poll, when 46 percent said they backed it and 44 percent were opposed.
Most readers of this blog are probably familiar with the concept of margin-of-error (MoE), the idea that because a poll interviews only a small (albeit scientifically selected) fraction of a large population, there’s likely going to be some fluctuation in a sample’s result from what the true value in the full population is.
In the present example, one probably doesn’t need a lot of statistical firepower to argue that this month’s 43% support for a public option (with its attendant margin of error in either direction) and last month’s 46% support (with its MoE) may not really represent much of a “shift.” For future reference, though, I thought I’d provide the formula for conducting a rigorous comparison of the sort implied by the NBC poll. This document from the University of Minnesota is very helpful. I’ve summarized some of the key ideas from the Minnesota page in the following graphic.
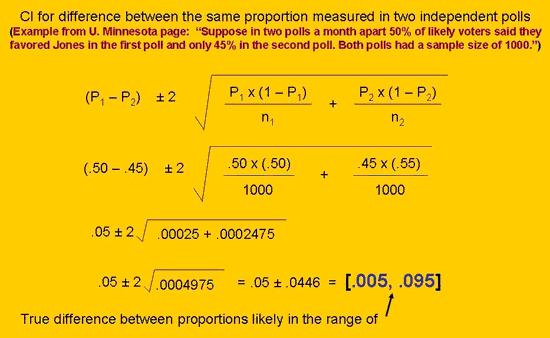
The formula leads us to a 95% Confidence Interval (CI) for what the true difference between the proportions is. In other words, the difference between the two Jones approval ratings is highly likely to be something greater than zero, but not necessarily much different from zero. (One would typically multiply the standard error by 1.96 to get the “plus/minus” term for a 95% confidence interval, but perhaps the Minnesota writer was trying to simplify things by using 2.)
Applying the above formula to the two NBC polls’ public-option support levels, one gets:
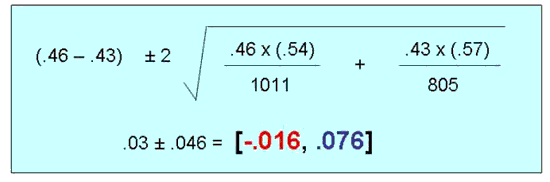
Because the CI is inclusive of zero (i.e., bounded by a negative value at one end and a positive value at the other), it is thus within the realm of possibility that the difference is indeed zero, as I implied above.
Disclaimer: This page contains affiliate links. If you choose to make a purchase after clicking a link, we may receive a commission at no additional cost to you. Thank you for your support!


Leave a Reply