The economic benefits and costs of mitigating global warming are widely debated. This column shows that based on current scientific knowledge and standard economic principles, a simple formula for the marginal damage of emissions can be constructed. The formula considerably strengthens the case for carbon taxation versus caps, allows straightforward calculation of the ‘global carbon debt’ rich nations owe to poor nations and future generations, and offers a yardstick for carbon capture and storage investments.
There now is widespread consensus that the key driver of climate change is the emission of carbon dioxide from burning fossil fuels (Metz et al. 2007). Since climate change affects the global economy, this is a textbook example of what economists label a ‘pure externality’. There is substantial uncertainty about how large this externality is. Yet, available knowledge can be used to provide an estimate of the externality that is surprisingly robust. In this note we argue that this provides a strong case for using a carbon tax rather than emission caps.
Recent research
Standard economic principles imply that the climate change externality of emitting carbon is determined by the following factors:
1. The damages caused by a marginal unit of carbon in the atmosphere.
2. How long a unit of carbon stays in the atmosphere.
3. How we evaluate future damages.
In recent work (Golosov et al. 2013), we show that this decomposition allows us to derive a simple formula for the optimal carbon tax. Importantly, we show that this formula is robust across a large range of climate models that differ in their assumptions on technical advances, population growth, and many other features of the global economy – including most existing climate models. The robustness came as a major surprise to us and is, we believe, an important finding.
Our simple marginal damage formula
The optimal carbon tax formula relies on the following insights.
First, the overall mapping from atmospheric carbon concentration to the flow of economic damages is approximately linear when the damages are expressed as a share of global GDP. The linearity reflects:
- The convexity in the mapping – developed by Nordhaus – from global mean temperature to damages measured as a percentage of GDP; and
- The concavity in the mapping between CO2 concentration and temperature.1
These two non-linearities approximately cancel.
- The result is a flow-damage elasticity of about 0.0025% of global GDP per gigaton of carbon.
Given the fact that there is now around an extra 200 gigatons in the atmosphere, the total flow loss is around 0.5% of global GDP.
Second, a good approximation to the carbon cycle is that 50% of the emitted carbon is quickly absorbed by plants and the upper layers of the ocean, while 20% stays for thousands of years. The remainder trickles down to the deep oceans at a rate of a few percent per decade (See Metz et al. 2007 and Archer 2005).
Third, the current discounted value of future damages is independent of future levels of GDP (and hence of population and any determinants of GDP, such as technological change) under two additional assumptions:
- Marginal utility is inversely proportional to consumption; and
- The consumption/output ratio is constant.
These assumptions are typical of most macroeconomic calibrations, and incorporate risk aversion. A large number of robustness checks show that only major – and, we argue, unreasonable – departures from these assumptions could significantly alter the results we report.
Using these properties, it is straightforward to show that the externality and thus the optimal carbon tax is proportional to:
- Current global GDP,
- The expected flow damage elasticity, and
- The discounted duration of carbon in the atmosphere (see Golosov et al. 2014 or, for a less technical presentation, Hassler and Krusell 2014).
The result is a simple closed-form formula for optimal tax.
In Figure 1 below, we depict the optimal carbon tax as a function of the subjective discount rate. This parameter can be thought of as representing the down-weighting of the welfare of future generations.
Figure 1. Optimal carbon tax as a function of the subjective discount rate
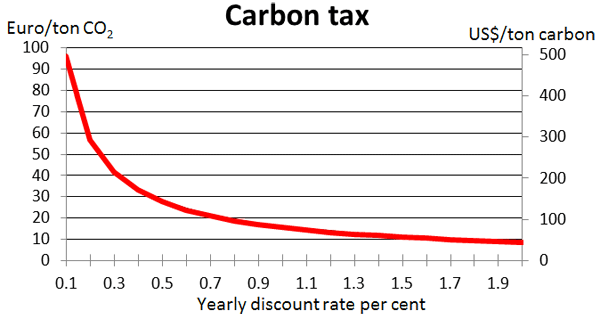
The key point is that the required tax is not dramatic. Even if a subjective discount rate lower than that usually used in macroeconomic studies is applied, the tax rate is not above the current carbon tax used in Sweden, for example, and it is not high enough so as to seriously threaten worldwide economic growth.
The costs and difficulties associated with a given quantity cap
It is much more difficult to say how large the reductions in fossil-fuel emissions would be as a result of introducing the optimal level of carbon taxation. The answer depends on the costs of mitigation, which depend on future technological developments, and are expected to vary over time and between different economies. This uncertainty is a major challenge for the quantity-based policy approach, as illustrated by the collapse of the price of emission rights in the EU trading scheme.
It may seem a priori reasonable to try to limit the temperature increase to two degrees Celsius, the approach currently taken, with the associated implication for a global cap on the allowed carbon emissions. But the two-degree target is not based on cost-benefit calculations, and in particular not knowing the mitigation costs – which differ markedly by country – makes a cap hard to agree on. In fact, the current global target amounts to a zero-sum game whereby all countries individually try to minimise their own caps. This zero-sum game is bound to fail.
Policy implications
There are three key insights arising from our analysis:
- First, our comparison between a carbon tax, based on our robust and transparent formula, and a carbon cap, rather considerably strengthens the case in favour of carbon taxation.
We thus propose to put a carbon tax back on the agenda for the next round of climate negotiations.
- Second, our formula allows a straightforward (and robust) way of computing the ‘global carbon debt’ due to accumulated previous emissions, and largely owed by the world’s currently developed nations to the rest of the world and to future generations.2
The global carbon debt of course depends on the subjective discount rate. With a discount rate of 1%, our formula suggest that it is – roughly speaking – 40% of annual world GDP (or the sum of US and EU GDP).
- Third, the formula offers a yardstick for carbon capture and storage investments.
Our conclusion
We see a more promising future in striving to agree on a uniform global carbon tax. We have argued that its optimal value can be robustly computed and its main subjective element – the intergenerational discount rate – should not be a cause of significant disagreement across countries.
Our formula can calculate the discounted value of damages that will occur in the future due to all the fossil carbon emitted so far. To us it appears reasonable that the countries responsible for past emissions – largely the developed world – should acknowledge this debt. It also appears reasonable that mortgages on the debt be paid to a fund aimed at helping poor countries deal with adaptation.
The practical implementation of a global tax may be challenging, especially in countries that rely less on markets than does the developed world. But using the tax as an explicit extra cost, or price tag, in any decisions to use fossil fuel represents a practical mind-set. Similarly, any investments in carbon capture and storage that, per unit, cost more than the tax should not be undertaken. In short, the plan to introduce a global carbon tax seems to have a chance of succeeding, while the current attempts to agree on a two-degree warming cap have, for understandable reasons, proven rather futile.
References
•Archer, David (2005), “The Fate of Fossil Fuel CO2 in Geologic Time”, Journal of Geophysical Research, 110.
•Arrhenius, Svante (1896), “On the Influence of Carbonic Acid in the Air upon the Temperature of the Ground”, Philosophical Magazine and Journal of Science, 41(5): 237–276.
•Golosov, Mikhail, John Hassler, Per Krusell, and Aleh Tsyvinski (2014), “Optimal Taxes on Fossil Fuel in General Equilibrium”, Econometrica, forthcoming.
•Hassler, John and Per Krusell (2014), “The Economy and the Climate”, Mistra-SWECIA Report No 5.
•Metz, Bert, Ogunlade Davidson, Peter Bosch, Rutu Dave, and Leo Meyer, eds. (2007), “Climate Change 2007: The Physical Science Basis”, Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change.
______
1 Arrhenius (1896) found a log-linear relation between temperature and CO2 concentration that remains a good approximation to the output of currently used global climate models. Due to limited knowledge about the strength of a large number of different feedback mechanisms, there is substantial uncertainty about the strength of this relationship, but according to the latest IPCC report, a doubling of the CO2 concentration is likely to increase the global mean temperature by 1.5 to 4.5 degrees. Stronger non-linearities – such as a global tipping point – cannot be ruled out entirely, but there is nothing close to a consensus on the nature of such a tipping point. Local tipping points are well known, but do not seem to aggregate so as to violate the approximate log-linearity.
2 Calculation available at http://hassler-j.iies.su.se/papers/carbondebt.pdf
Leave a Reply